(this is part 1 of the “AI for Finance Course“)
Imitating nature is always a good way to make technical progress. Airplanes copied birds, submarines copied fish, and neural networks copied the brain. 🧠
Or at least they were inspired by it.

The left side represents sensory inputs where signals are received. And the right side represents the output where signal is emitted.
Obviously, not every input is equally important.
You also know this from personal experience. You do not “absorb” or accept all information in the same way. For example, a message from a close friend will have a greater impact on you than if it was from a complete stranger.
This is where a familiar neuron model (perceptron) comes from:
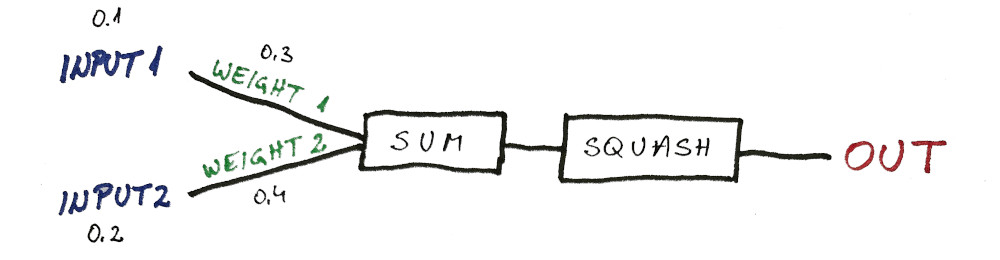
There are 2 main things a neural network (or a single neuron) has to do:
- 1) generating output
- 2) learning from mistakes
- plus we need to test the neuron
Generating Output
Each input has its importance indicated by the weight. If the input (data) is deemed unimportant, the weight will be zero. (because any input multiplied by zero will be zero)
And if the input is extremely important the weight will be a million. (and all the combinations in between)
Since the weights could go into crazy numbers, it is important to keep the outputs in check. We do this by “squashing” every output between zero and one.
Also notice that this is not really a problem when we have a “single neuron system”. The problem comes when this “wild” neuron is part of a network of neurons.
Not to mention (as the outputs propagate through the layers) we could quickly reach computer limits and the numbers would not fit into variables. And this could lead to bugs and overflow (which we might not even detect).
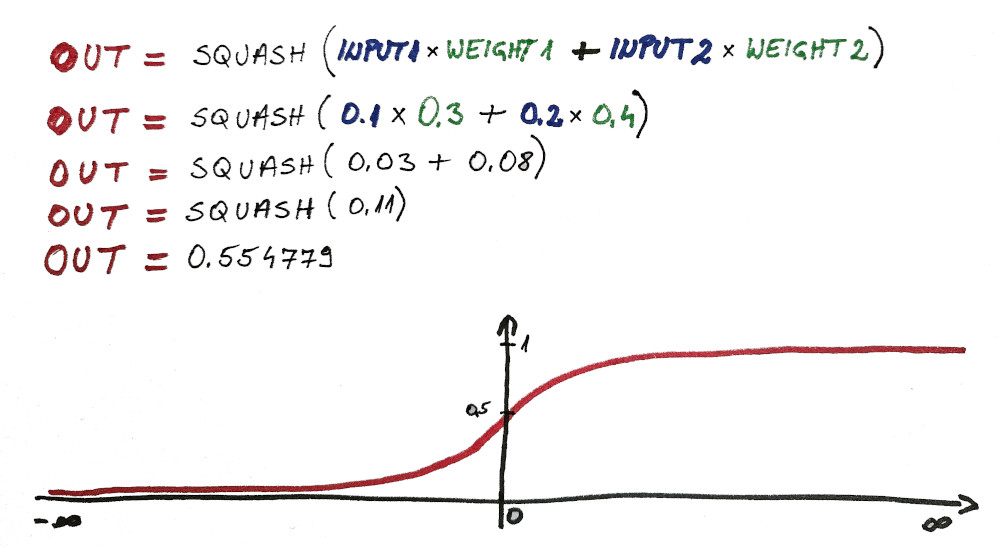
To “squash” the output, we usually apply some type of sigmoid function that transforms any input from negative infinity to infinity and outputs a manageable number (from zero to one).
double sigmoid(double input) { return (tanh(input) + 1) / 2.0; }
Here is a simple calculation of the output:
(plus the neuron model as a reminder)

And here is how this looks like in the code:
double getPrediction(double[] inputs) { double[2] weightedInputs = inputs[] * weights[]; double weightedSum = weightedInputs.array.sum; double prediction = sigmoid(weightedSum); return prediction; }
Learning From Mistakes
In the example above you can see that the only part we have any control over are the weights. You can also see that I just made them up randomly. Basically, they are meaningless and this network is not very smart.
But now we’re going to fix that…
Let’s say this network is going to predict whether we should buy or sell a stock from a (fictional) agricultural company AgroX.
This company stock goes up on the years when the crops are doing well. And this happens when there’s a lot of sun and rain.
In our example neuron:
- INPUT 1 –> temperature percentile in the last n years
- INPUT 2 –> rain percentile in the last n years

As you can see this was a very bad year for this company:
- temperature was in the bottom 10% in the last n years
- and rain was in the bottom 20% in the last n years
This means it was extremely cold and very dry this year. So the crops will be terrible and company earnings even worse.
So ideally, our neuron (perceptron) should have said to sell the 💩 out of this company (i.e. output should have been zero).
Instead, output was 0.554479
And that was an error.
But, just as we learn from our mistakes we want our network to learn from them as well.
So how do we do that?
First, we’re going to take the error and use it to correct the weights. Each weight is updated proportionally to the strength to the input.
Think about it… this is just like in real life…
The person who screamed the loudest telling you the wrong info is going to lose your trust the most.
(compared to someone who just humbly said “I think this might be correct, but I’m not really sure”)
In our case, INPUT2 (the rain) was the loudest (0.2) and you will see that WEIGHT2 will be changed the most.

OUT = 0.554779
CORRECT = 0 // you should sell
ERROR = OUT - CORRECT
ERROR = 0.554779 - 0
ERROR = 0.554779
CORRECTION1 = INPUT1 x ERROR
CORRECTION1 = 0.1 x 0.554779
CORRECTION1 = 0.0554779
NEW_WEIGHT1 = WEIGHT1 - CORRECTION1
NEW_WEIGHT1 = 0.3 - 0.0554779
NEW_WEIGHT1 = 0.2445221
CORRECTION2 = INPUT2 x ERROR
CORRECTION2 = 0.2 x 0.554779
CORRECTION2 = 0.1109558
NEW_WEIGHT2 = WEIGHT1 - CORRECTION1
NEW_WEIGHT2 = 0.4 - 0.1109558
NEW_WEIGHT2 = 0.2890442And that’s it!
Now our network is better at predicting AgroX stock price than it was before.
Of course, to be (much) better we need to…
- feed it more data
- and/or make more passes through this data
…but each loop will have the same process in the background… itching closer to the best possible solution that the network (or the single neuron) can provide.
Here is how this looks like in the code:
void updateWeights(double prediction, double[] inputs, double output) { double error = prediction - output; double[2] errorCorrections = inputs[] * error; weights[] -= errorCorrections[]; }
But…
…how do we even know the neuron is doing better now?
Testing The Neuron
Well, it is quite simple actually –> we can feed it original inputs and see if the error is now lower. And if the error is lower, we know that our neuron is better.
This means our error needs to be lower than 0.554779
So we’re just doing the same thing as we did at the beginning with random weights (we’re just going to use the updated weights now).

OUT = SQUASH(INPUT1 x NEW_WEIGHT1 + INPUT2 x NEW_WEIGHT2)
OUT = SQUASH(0.1 x 0.2445221 + 0.2 x 0.2890442)
OUT = SQUASH(0.02445221 + 0.05780884)
OUT = SQUASH(0.08226105)
OUT = 0.541038
NEW_ERROR = OUT - CORRECT
NEW_ERROR = 0.541038
OLD_ERROR = 0.554779
NEW_ERROR < OLD_ERRORSince new error is lower than the previous one, we can confirm that our network actually learned something.
Now it’s just a matter of more data and more iterations to make it better at predicting AgroX stock performance.
Below is the full code:
import std.stdio : pp = writeln; import std.algorithm : sum; import std.array : array; import std.math.trigonometry : tanh; double[] weights = [0.3, 0.4]; double[][] inputs = [ [0.1, 0.2], // 0 - bad year - sell [0.5, 1.0], // 1 - avg temp & best rain - buy [1.0, 0.5], // 1 - best temp & avg rain - buy [1.0, 1.0], // 1 - best temp & best rain - BUY [0.0, 0.0], // 0 - worst year on record - SELL!!! // unfortunately this neuron could never learn // at least not from all the data // next lesson will show you how to fix it ]; double[] outputs = [0, 1, 1, 1, 0]; double sigmoid(double input) { return (tanh(input) + 1) / 2.0; } void updateWeights(double prediction, double[] inputs, double output) { double error = prediction - output; pp("error: ", error); double[2] errorCorrections = inputs[] * error; weights[] -= errorCorrections[]; pp("weights: ", weights); } double getPrediction(double[] inputs) { double[2] weightedInputs = inputs[] * weights[]; double weightedSum = weightedInputs.array.sum; double prediction = sigmoid(weightedSum); return prediction; } void trainNetwork() { for (int n = 0; n < 1000; n++) { // 1000 times through the data for (int i = 0; i < inputs.length; i++) { double prediction = getPrediction(inputs[i]); updateWeights(prediction, inputs[i], outputs[i]); } } } void main() { pp("weights: ", weights); trainNetwork(); // TESTING pp(); pp(inputs[0], " : ", getPrediction(inputs[0])); pp(inputs[1], " : ", getPrediction(inputs[1])); pp(inputs[2], " : ", getPrediction(inputs[2])); pp(inputs[3], " : ", getPrediction(inputs[3])); pp(inputs[4], " : ", getPrediction(inputs[4])); pp(); }
But there is one big problem –> our neuron cannot learn from all the data because it has one key part missing.
As you can see it has difficulty learning from the data whose values are close to zero.
(even after 1000 iterations)
In the next lesson, I’m going to show you how to fix this problem.
// [0.1, 0.2] : 0.612728 <-- problem // [0.5, 1] : 0.908376 // [1, 0.5] : 0.999506 // [1, 1] : 0.998647 // [0, 0] : 0.5 <-- problem
NEXT LESSON:
Crucial Part of The Neuron